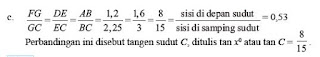QUIZ TRIGONOMETRI

Untuk mengetahui sejauh mana pemahaman tentang trigonometri, silahkan akses Quiz berikut.

Quiz

LINGKARAN SATUAN

Untuk menentukan nilai perbandingan trigonometri selain sudut-sudut istimewa, selain dengan menggunakan tabel trigonometri atau kalkulator dapat pula menggunakan lingkaran satuan.

Caranya?

Bisa kita simak dari video berikut.

courtesy of YouTube.

Lembar Kerja Siswa

Berikut adalah Lembar Kerja Siswa (LKS) yang dapat digunakan sebagai latihan dalam mempelajari materi trigonometri.

LKS Trigonometri

GRAFIK FUNGSI TRIGONOMETRI

Grafik fungsi trigonometri adalah penyajian fungsi trigonometri ke dalam bentuk diagram Cartesius. 

Persamaan dan perbedaan antara grafik fungsi sinus, grafik fungsi kosinus dan grafik fungsi tangen.

1. Persamaan grafik fungsi sinus, cosinus, dan tangen adalah ketiganya merupakan fungsi berkala atau fungsi periodik yang berulang untuk periode tertentu.
2. Perbedaan grafik fungsi sinus, cosinus, dan tangen adalah sebagai berikut:

b.  Menggunakan software geogebra

Dengan menggunakan software, kita dapat secara langsung menerangkan dan menunjukkan perubahan-perubahan yang terjadi pada grafik fungsi trigonometri bentuk baku bila dimodifikasi. 

Untuk lebih jelasnya, bisa dilihat dari video pengembangan dari screen cast o matic yang sudah saya buat sebagai berikut:

PERSAMAAN TRIGONOMETRI

Persamaan trigonometri adalah persamaan yang memuat perbandingan trigonometri dengan variabel sudut x (dalam ukuran derajat atau radian).

Beberapa hal yang harus diperhatikan dalam mengerjakan suatu persamaan trigonometri adalah nilai x pada suatu persamaan trigonometri akan berulang berdasarkan periode dari fungsinya, baik sinus, cosinus, maupun tangen. Sehingga, setiap mencari penyelesaian dari persamaan trigonometri, untuk persamaan sinus dan kosinus harus dikalikan dengan k.360^o dan untuk persamaan tangen dikalikan dengan k.180 ^o karena fungsi sinus, kosinus dan tangen merupakan fungsi periodik yang akan terus berulang pada suatu periode tertentu, yaitu 360^o untuk fungsi sinus dan fungsi kosinus dan 180^o untuk fungsi tangen.

Pernahkah kamu melihat persamaan seperti persamaan berikut: 

   

 

  

Persamaan tersebut dinamakan dengan persamaan trigonometri karena memuat fungsi trigonometri. 

Bagaimana cara menyelesaikan persamaan trigonometri tersebut? 

Sebelum mempelajarinya, mari kita ingat kembali tentang grafik fungsi trigonometri dan sudut-sudut berelasi. Grafik fungsi sinus dan kosinus berulang setiap 360^o, sedangkan grafik fungsi tangen berulang setiap 180^o. Selain itu, kita juga telah mempelajari tentang sudut berelasi di kuadran I, kuadran II, kuadran III maupun kuadran IV. Dengan berbekal konsep grafik fungsi trigonometri dan sudut berelasi, kita akan dapat menyelesaikan suatu persamaan trigonometri. Mari kita lanjutkan dengan mempelajari persamaan trigonometri berikut. 

Contoh: 

IDENTITAS TRIGONOMETRI

Identitas trigonometri adalah suatu bentuk trigonometri yang dinyatakan dalam bentuk trigonometri yang lain. Identitas trigonometri dasar merupakan hubungan kebalikan, perbandingan dan teorema Phytagoras.

1. Identitas Trigonometri dasar yang merupakan hubungan kebalikan

  

 

 

2. Identitas Trigonometri dasar yang merupakan hubungan perbandingan

  

  

3. Identitas Trigonometri dasar yang diperoleh dari teorema Phytagoras

 

 

  

Beberapa hal yang harus diperhatikan ketika membuktikan suatu identitas trigonometri, yaitu:

1. Setelah mengetahui kedelapan identitas trigonometri dasar di atas, selanjutnya kita akan menggunakan identitas-identitas tersebut, bersama dengan pengetahuan kita mengenai aljabar, untuk membuktikan identitas-identitas lainnya.
2. Ingat bahwa identitas trigonometri merupakan pernyataan yang memuat kesamaan dua bentuk untuk setiap penggantian variabelnya dengan nilai di mana bentuk tersebut didefinisikan. Untuk membuktikan identitas trigonometri, kita gunakan substitusi trigonometri dan manipulasi aljabar dengan tujuan mengubah bentuk pada ruas kiri identitas menjadi bentuk seperti pada ruas kanan, atau sebaliknya.
3. Satu hal yang harus diperhatikan dalam membuktikan identitas trigonometri adalah kita harus bekerja pada masing-masing ruas secara terpisah. Kita tidak boleh menggunakan sifat-sifat aljabar yang melibatkan kedua ruas identitas—seperti sifat penjumlahan kedua ruas persamaan. Karena, untuk melakukan hal tersebut, kita harus menganggap bahwa kedua ruas sudah sama, yang merupakan suatu hal yang akan kita buktikan. Intinya, kita tidak boleh memperlakukan masalah sebagai suatu persamaan.

Cara menyusun langkah pembuktian sebuah identitas trigonometri dengan menggunakan rumus-rumus trigonometri adalah:

1. Biasanya akan lebih mudah jika memanipulasi ruas persamaan yang lebih rumit terlebih dahulu.
2. Carilah bentuk yang dapat disubstitusi dengan bentuk trigonometri yang ada dalam identitas trigonometri, sehingga didapatkan bentuk yang lebih sederhana.
3.  Perhatikan operasi-operasi aljabar, seperti penjumlahan pecahan, sifat distributif, atau pemfaktoran, yang mungkin dapat menyederhanakan ruas yang kita manipulasi, atau minimal dapat membimbing kita kepada bentuk yang dapat disederhanakan.
4. Jika tidak tahu apa yang harus dilakukan, ubahlah semua bentuk trigonometri menjadi bentuk sinus dan cosinus. Mungkin hal tersebut bisa membantu.
5. Selalu perhatikan ruas persamaan yang tidak dimanipulasi untuk memastikan langkah-langkah yang kita lakukan menuju bentuk dalam ruas tersebut.

Contoh:

KOORDINAT KUTUB/ POLAR DAN KOORDINAT CARTESIUS

Contoh:

NILAI PERBANDINGAN TRIGONOMETRI DI BERBAGAI KUADRAN

1. Pembagian sudut dalam trigonometri

2. Sudut-sudut Berelasi
Pada awal subbab ini, akan dikaji nilai sinus, cosinus, tangen dan kebalikannya untuk domain sudut dalam satuan derajat atau radian. Selain itu, nilai semua perbandingan tersebut juga akan kita pelajari pada setiap kuadran dalam koordinat Kartesius. Mari kita pahami melalui pembahasan berikut ini.

Misalkan titik A (x, y), panjang OA = r dan sudut AOX = α. Mari kita perhatikan gambar di atas, dari segitiga siku-siku yang terdapat di kuadran I, berlaku :

Dengan mempertimbangkan semua kombinasi koordinat titik pada koordinat Kartesius, kita dapat telusuri perbedaan tanda untuk ketiga perbandingan trigonometri yang utama.

Garis putus-putus pada gambar menyatakan projeksi OA ke setiap sumbu, misalnya pada Gambar 8.15(a), garis putus-putus adalah proyeksi sumbu Y di kuadran II. Sedangkan garis putus-putus melengkung menyatakan besar sudut yang besarnya sama, misalnya, pada Gambar 8.15 (b), garis putus-putus melengkung menyatakan dua sudut yang besarnya sama.
Hubungan dari nilai perbandingan sudut-sudut berelasi pada setiap kuadran ditunjukkan sebagai berikut:

NILAI PERBANDINGAN TRIGONOMETRI UNTUK SUDUT-SUDUT ISTIMEWA

Sudut-sudut istimewa adalah sudut yang besarnya 30⁰, 45 ⁰, 60⁰ , dan kelipatannya. Nilai-nilai perbandingan Trigonometrinya dapat ditentukan tanpa harus menggunakan alat bantu kalkulator atau tabel, tapi dapat ditentukan dengan bantuan segitiga siku-siku tertentu yang membentuk sudut tersebut. Segitiga-segitiga siku-siku tersebut sebagai berikut:

Perbandingan trigonometri sudut-sudut istimewa tersebut dapat dituliskan sebagai berikut:

PERBANDINGAN TRIGONOMETRI PADA SEGITIGA SIKU-SIKU

Pada peradaban kehidupan budaya Dayak, kajian mengenai trigonometri sudah tercermin dari berbagai ikon kehidupan mereka. Misalnya, para arsitekturnya, sudah menerapkan kesetimbangan bangunan pada rumah adat yang mereka ciptakan. Rumah adat tersebut berdiri kokoh sebagai hasil hubungan yang tepat antara besar sudut yang dikaitkan dengan panjang sisi-sisinya. Apakah para Arsitektur tersebut mempelajari trigonometri juga?

Coba kita pahami deskripsi berikut.

Pak Yahya adalah seorang penjaga sekolah. Tinggi pak Yahya adalah 1,6 m. Dia mempunyai seorang anak, namanya Dani. Dani masih kelas II Sekolah Dasar. Tinggi badannya 1,2 m. Dani adalah anak yang baik dan suka bertanya. Dia pernah bertanya kepada ayahnya tentang tinggi tiang bendera di lapangan itu. Dengan senyum, Ayahnya menjawab 8 m. Suatu sore, disaat dia menemani ayahnya membersihkan rumput liar di lapangan, Dani melihat bayangan setiap benda ditanah. Dia mengambil tali meteran dan mengukur panjang bayangan ayahnya dan panjang bayangan tiang bendera, yaitu 3 m dan 15 m. Tetapi dia tidak dapat mengukur panjang bayangannya sendiri karena bayangannya mengikuti pergerakannya. Jika kamu sebagai Dani, dapatkah kamu mengukur bayangan kamu sendiri?

Konsep kesebangunan pada segitiga terdapat pada cerita tersebut. Mari kita gambarkan segitiga sesuai cerita di atas.

KONSEP DASAR SUDUT

Dalam kajian geometris, sudut didefinisikan sebagai hasil rotasi dari sisi awal (initial side) ke sisi akhir (terminal side). Selain itu, arah putaran memiliki makna dalam sudut. Suatu sudut bertanda “positif” jika arah putarannya berlawanan dengan arah putaran jarum jam, dan bertanda “negatif” jika arah putarannya searah dengan jarum jam. Arah putaran untuk membentuk sudut juga dapat diperhatikan pada posisi sisi akhir terhadap sisi awal. Untuk memudahkannya, mari kita cermati deskripsi berikut ini.

Dalam bidang koordinat kartesius, jika sisi awal suatu garis berimpit dengan sumbu x dan sisi terminalnya terletak pada salah satu kuadran pada koordinat kartesius itu, disebut sudut standar (baku). Jika sisi akhir berada pada salah satu sumbu pada koordinat tersebut, sudut yang seperti ini disebut pembatas kuadran, yaitu 0°, 90°, 180°, 270° dan 360°. Sebagai catatan, bahwa untuk menyatakan suatu sudut, lazimnya digunakan huruf Yunani, seperti, α (alpha), β ( betha), γ (gamma), dan θ (tetha), dan juga digunakan huruf-huruf kapital, seperti A, B, C, dan D.

Cermati gambar di bawah ini.

Jika sudut yang dihasilkan sebesar α (sudut standar), maka sudut β disebut sebagai sudut koterminal, sehingga α + β - 360^O, seperti gambar berikut.

SATUAN UKURAN SUDUT

Pernahkah kamu memperhatikan gerakan gelombang laut sampai ke pinggir pantai/ dinding suatu pelabuhan? Tahukah kamu bagaimana cara mengukur kedalaman laut/samudera? Fenomena nyata ini merupakan sebagain dari penerapan trigonometri dalam kehidupan nyata. Dalam bidang fisika, teknik, dan kedokteran, trigonometri mengambil peranan penting dalam pengembang teknologi kedokteran dan teori-teori fisika dan teknik. Dalam Matematika, trigonometri digunakan untuk menemukan relasi antara sisi dari sudut pada suatu segitiga.

 

A.      Ukuran Sudut (Derajat dan Radian)

Pada umumnya, ada dua ukuran yang digunakan untuk menentukan besar suatu sudut, yaitu derajat dan radian. Tanda ““ dan “rad” berturut-turut menyatakan simbol derajat dan radian. Singkatnya, satu putaran penuh = atau  didefinisikan sebagai besar sudut yang dibentuk oleh    putaran penuh. Cermati gambar berikut ini!

 

Tentunya, dari Gambar 8.1, kita dapat mendeskripsikan untuk beberapa satuan putaran yang lain. Sebelum kita memahami hubungan “derajat dengan radian”, mari kita pelajari kajian berikut ini.

Satu radian diartikan sebagai ukuran sudut pusat α suatu lingkaran yang panjang busurnya sama dengan jari-jari, perhatikan Gambar 8.2.

 

Jika besar

Jika panjang busur tidak sama dengan r, maka cara menentukan besar sudut tersebut dalam satuan radian diselesaikan menggunakan definisi perbandingan:

 

Lebih lanjut, hubungan satuan derajat dengan satuan radian, bahwa 1 putaran penuh sama dengan 2π rad. Seperti dinyatakan dalam definisi berikut

 

Contoh:

 

 

PENERAPAN RUMUS SINUS-COSINUS 1

Silabus Matematika SMA-SMK Wajib

Berikut adalah file silabus mata pelajaran Matematika Wajib tingkat SMA/SMK.

Silabus Matematika SMA Wajib